As Thomas Sargent said:
“A rational expectations equilibrium model is a likelihood function”
However in many cases, the likelihood function is too complicated to be written down in closed form. To estimate the structural parameters of a given model, one can still use Monte-Carlo methods. In this post, I would like to describe the simulated method of moments (SMM), which is a widely used simulation-based estimation technique.
A Simple Setting
I want to illustrate the SMM in one of the simplest settings you could think of: the estimation of the mean of a normal density with known variance. Let’s say we have access to a (bi-dimensional) time series and we suspect it to be normally distributed with mean $[a,\,b]‘$ and variance the identity matrix $\mathcal{N}([a,\,b]‘,\,I_2)$. Let’s pretend that we have no idea on how to write down the associated likelihood function. The good news is that if we have access to a “black box” that generates $i.i.d$ draws from the law $\mathcal{N}([c,\,d]‘,\,I_2)$, it is enough for us to do inference.
SMM is GMM
The SMM estimator can be viewed as an extension of GMM. The difference being that the function mapping the set of parameters to moments has no closed-form expression. Mathematically, we want to minimize the following objective function:
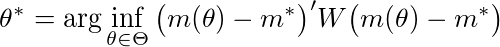
where $m^*$ is a vector empirical moments, $m(\theta)$ a vector of the same moments calculated using simulated data when the structural parameters are equal to $\theta$, and $W$ a weighing matrix.
The SMM estimate is such that the (weighted) distance between simulated and empirical moments is minimized. This estimator is quite intuitive: under the hypothesis that the model is correctly specified, it should be able to reproduce empirical moments when parameters values are equal to the “true” ones.
Inference
Under some regularity conditions (see McFadden 1989), the extra noise introduced by simulation is not problematic and inference is possible. That is, we can build a confidence intervals for the SMM estimates.
Implementation in Julia
The code below shows how one can recover the true parameters of the Normal density $\mathcal{N}([a,\,b]‘,\,I_2)$. I use the MomentOpt package, which relies on some refinements of the MCMC method to explore the state-space with several Markov chains in parallel. These Markov chains communicate between themselves to avoid being stuck in a local mode of the posterior distribution. In practice, I choose 5 Markov chains. Figure 1 shows the realizations for the first chain. As illustrated in Figure 2, we successfully recovered the true values for $a$ and $b$. For each chain, the quasi-posterior mean and median for $a$ and $b$ are extremely close to the true values $1$ and $-1$.
Figure 1
 |
|---|
| History of one chain |
Figure 2
 |
|---|
| Histograms for the 5 chains |
#---------------------------------------------------------------------------------------------------------
# Julien Pascal
# last edit: 12/02/2018
#
# Julia script that shows how the simulated
# method of moments can be used in a simple
# setting: estimation of the mean of a Normal r.v.
#
# I use the package MomentOpt: https://github.com/floswald/MomentOpt.jl
#
# Code heavily based on the file https://github.com/floswald/MomentOpt.jl/blob/master/src/mopt/Examples.jl
#----------------------------------------------------------------------------------------------------------
using MomentOpt
using GLM
using DataStructures
using DataFrames
using Plots
#plotlyjs()
pyplot()
#------------------------------------------------
# Options
#-------------------------------------------------
# Boolean: do you want to save the plots to disk?
savePlots = true
# initialize the problem:
#------------------------
# initial values:
#----------------
pb = OrderedDict("p1" => [0.2,-3,3] , "p2" => [-0.2,-2,2] )
# moments to be matched:
#-----------------------
moms = DataFrame(name=["mu1","mu2"],value=[-1.0,1.0], weight=ones(2))
"""
objfunc_normal(ev::Eval)
GMM objective function to be minized.
It returns a weigthed distance between empirical and simulated moments
copy-paste of the function objfunc_norm(ev::Eval)
I only made minor modifications to the original fuction
"""
function objfunc_normal(ev::Eval)
start(ev)
# extract parameters from ev:
#----------------------------
mu = collect(values(ev.params))
# compute simulated moments
#--------------------------
# Monte-Carlo:
#-------------
ns = 10000 #number of i.i.d draws from N([a,b], sigma)
#initialize a multivariate normal N([a,b], sigma)
#using a = mu[1], b=mu[2]
sigma = [1.0 ;1.0]
randMultiNormal = MomentOpt.MvNormal(mu,MomentOpt.PDiagMat(sigma))
simM = mean(rand(randMultiNormal,ns),2) #mean of simulated data
simMoments = Dict(:mu1 => simM[1], :mu2 => simM[2])#store simulated moments in a dictionary
# Calculate the weighted distance between empirical moments
# and simulated ones:
#-----------------------------------------------------------
v = Dict{Symbol,Float64}()
for (k, mom) in dataMomentd(ev)
# If weight for moment k exists:
#-------------------------------
if haskey(MomentOpt.dataMomentWd(ev), k)
# divide by weight associated to moment k:
#----------------------------------------
v[k] = ((simMoments[k] .- mom) ./ MomentOpt.dataMomentW(ev,k)) .^2
else
v[k] = ((simMoments[k] .- mom) ) .^2
end
end
# Set value of the objective function:
#------------------------------------
setValue(ev, mean(collect(values(v))))
# also return the moments
#-----------------------
setMoment(ev, simMoments)
# flag for success:
#-------------------
ev.status = 1
# finish and return
finish(ev)
return ev
end
# Initialize an empty MProb() object:
#------------------------------------
mprob = MProb()
# Add structural parameters to MProb():
# specify starting values and support
#--------------------------------------
addSampledParam!(mprob,pb)
# Add moments to be matched to MProb():
#--------------------------------------
addMoment!(mprob,moms)
# Attach an objective function to MProb():
#----------------------------------------
addEvalFunc!(mprob, objfunc_normal)
# estimation options:
#--------------------
# number of iterations for each chain
niter = 1000
# number of chains
nchains = 5
opts = Dict("N"=>nchains,
"maxiter"=>niter,
"maxtemp"=> 5,
# choose inital sd for each parameter p
# such that Pr( x \in [init-b,init+b]) = 0.975
# where b = (p[:ub]-p[:lb])*opts["coverage"] i.e. the fraction of the search interval you want to search around the initial value
"coverage"=>0.025, # i.e. this gives you a 95% CI about the current parameter on chain number 1.
"sigma_update_steps"=>10,
"sigma_adjust_by"=>0.01,
"smpl_iters"=>1000,
"parallel"=>true,
"maxdists"=>[0.05 for i in 1:nchains],
"mixprob"=>0.3,
"acc_tuner"=>12.0,
"animate"=>false)
# plot slices of objective function
#---------------------------------
s = doSlices(mprob,30)
# plot objective function over param values:
#-------------------------------------------
p1 = MomentOpt.plot(s,:value)
if savePlots == true
Plots.savefig(p1, joinpath(pwd(),"slices_Normal1.svg"))
end
# plot value of moment :mu1 over param values
#--------------------------------------------
p2 = MomentOpt.plot(s,:mu1)
if savePlots == true
Plots.savefig(p2, joinpath(pwd(),"slices_Normal2.svg"))
end
# plot value of moment :mu2 over param values
#--------------------------------------------
p3 = Plots.plot(s,:mu2)
if savePlots == true
Plots.savefig(p3, joinpath(pwd(),"slices_Normal3.svg"))
end
#---------------------------------------
# Let's set-up and run the optimization
#---------------------------------------
# set-up BGP algorithm:
MA = MAlgoBGP(mprob,opts)
# run the estimation:
@time MomentOpt.runMOpt!(MA)
# show a summary of the optimization:
@show MomentOpt.summary(MA)
# Plot histograms for chains:
#----------------------------
p4 = histogram(MA.chains[1])
p5 = histogram(MA.chains[2])
p6 = histogram(MA.chains[3])
p7 = histogram(MA.chains[4])
p8 = histogram(MA.chains[5])
p9 = Plots.plot(p4, p5, p6, p7, p8, layout=(5,1), legend=false)
if savePlots == true
savefig(p9, joinpath(pwd(),"histogram.svg"))
end
# Plot the "history" of one chain:
#--------------------------------
p10 = plot(MA.chains[1])
if savePlots == true
savefig(p10, joinpath(pwd(),"history_chain_1.svg"))
end
# Realization of chain 1:
#-----------------------
dat_chain1 = MomentOpt.history(MA.chains[1])
# keep only accepted draws:
#-------------------------
dat_chain1 = dat_chain1[dat_chain1[:accepted ].== true, : ]
# Quasi Posterior mean
#---------------------
QP_mean_p1 = mean(dat_chain1[:p1])
QP_mean_p2 = mean(dat_chain1[:p2])
# Quasi Posterior median
#-----------------------
QP_median_p1 = median(dat_chain1[:p1])
QP_median_p2 = median(dat_chain1[:p2])