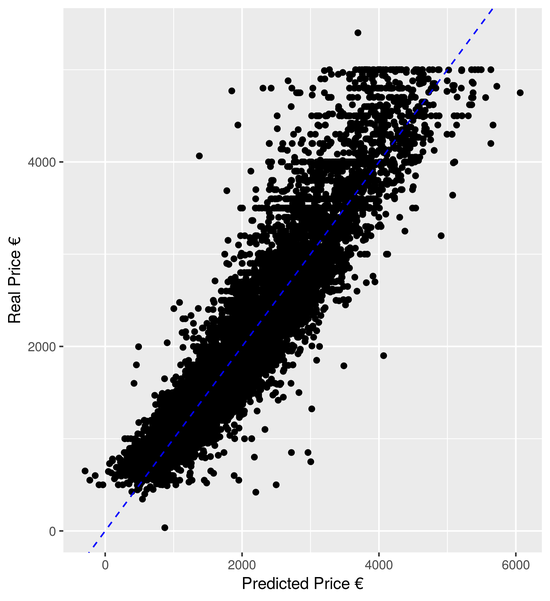
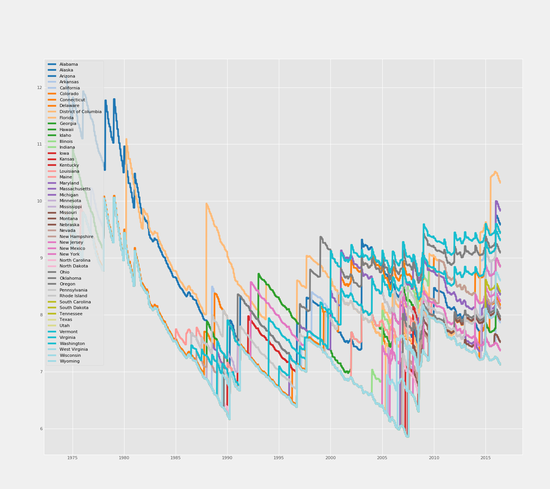
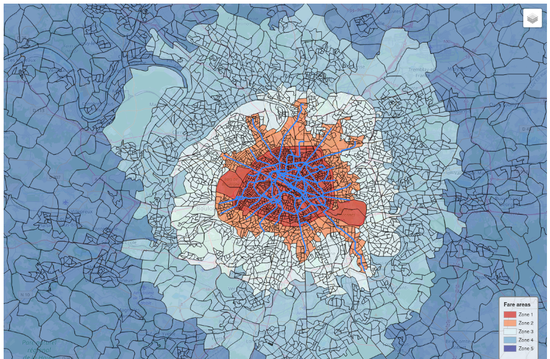
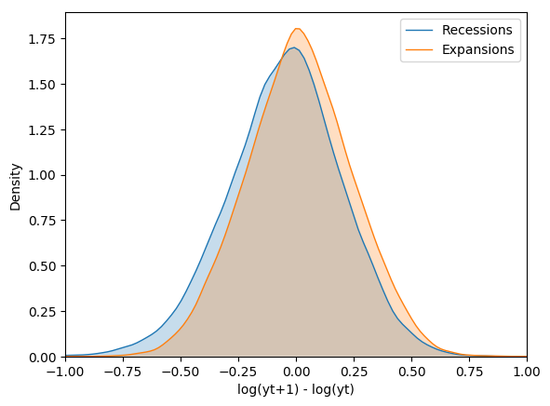
I am an Economist at the Central Bank of Luxembourg. I hold a PhD in Economics from Sciences Po.
The views expressed on this website are my own and do not necessarily represent the views of my employer.
Interests
- Labor Economics
- Macroeconomics
- Urban Economics
Education
-
Doctor of Philosophy - PhD, Economics, 2020
Sciences Po
-
Master's in Economics, 2016
Sciences Po
-
Bachelor of Mathematics, 2015
UPMC Sorbonne Universités
-
Bachelor of Social Sciences, 2013
Sciences Po